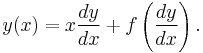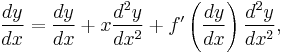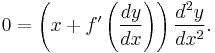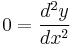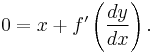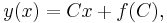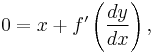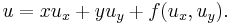Clairaut's equation
In mathematics, a Clairaut's equation is a differential equation of the form
To solve such an equation, we differentiate with respect to x, yielding
so
Hence, either
or
In the former case, C = dy/dx for some constant C. Substituting this into the Clairaut's equation, we have the family of functions given by
the so-called general solution of Clairaut's equation.
The latter case,
defines only one solution y(x), the so-called singular solution, whose graph is the envelope of the graphs of the general solutions. The singular solution is usually represented using parametric notation, as (x(p), y(p)), where p represents dy/dx.
This equation was named after Alexis Clairaut, who introduced it in 1734.
A first-order partial differential equation is also known as Clairaut's equation or Clairaut equation:
External links
- Clairaut, Alexis Claude (1736 (Année 1734)), "Solution de plusieurs Problemes où il s'agit de trouver des Courbes dont la propriété consiste dans une certaine relation entre leurs branches, exprimée par une Équation donnée.", Histoire de l'Académie royale des sciences: 196–215, http://gallica.bnf.fr/ark:/12148/bpt6k3531x/f344.table. At Gallica: the paper of Clairaut introducing the equation named after him.
- Rozov, N. Kh. (2001), "Clairaut equation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=C/c022350